Java 结构化并发
结构化并发(Structured Concurrency) 结构化并发是 Java 并发编程的重要演进方向,与虚拟线程紧密配合,旨在解决传统并发编程中的线程泄漏、错误处理困难等问题。 1. 历史背景 1.1 结构化并发的起源与核心类比 术语起源 “结构化并发”(Structured Concurrency)这个术语由 Martin Sústrik(ZeroMQ 作者)在 2016 年首次提出。随后,Nathaniel J. Smith 在 2018 年发表了著名的文章《Notes on structured concurrency, or: Go statement considered harmful》,系统性地阐述了结构化并发的理论基础。 timeline title 结构化并发发展历程 2016 : Martin Sústrik 首创术语 : 在 250bpm.com 发表系列文章 2018 : Nathaniel J. Smith 发表核心论文 : "Go statement considered ha...
G1/ZGC/Shenandoah 垃圾收集器对比
垃圾收集的核心挑战 垃圾收集器的设计始终面临三个核心指标的权衡:吞吐量、延迟和内存占用。这三个指标构成了一个不可能三角,优化其中一个指标往往需要牺牲其他指标。 吞吐量指单位时间内完成的工作量,通常用应用程序运行时间占总时间的比例来衡量。对于批处理任务、科学计算等场景,高吞吐量是首要目标。 延迟指垃圾收集造成的应用停顿时间。对于交互式应用、金融交易系统等对响应时间敏感的场景,低延迟至关重要。延迟通常关注最大停顿时间和停顿时间分布。 内存占用指垃圾收集器为了完成收集工作所需的额外内存空间。内存受限的环境下,收集器自身的内存开销成为关键约束。 传统垃圾收集器在三者之间做出明确取舍:Serial 和 Parallel GC 追求高吞吐量,但停顿时间较长;CMS GC 降低停顿时间,但牺牲吞吐量并占用更多内存。现代收集器试图在三者之间找到更优的平衡点。 G1(Garbage First)收集器 G1 收集器在 JDK 7u4 版本正式推出,是 JDK 9 之后的默认垃圾收集器。G1 的核心思想是打破传统分代收集的物理隔离,将堆内存划分为多个大小相等的 Region。 Region 化堆内存...
TLS 握手与加密通信
为什么需要 TLS HTTP 协议最初设计为明文传输协议,所有通信内容都以纯文本形式在网络中传输。这种设计在互联网早期是合理的,但随着网络应用的普及和敏感数据的增多,明文传输带来了严重的安全风险。 窃听风险 在明文传输模式下,任何能够访问网络链路的攻击者都可以轻易读取通信内容。这包括: 同一局域网内的其他用户 网络服务提供商(ISP) 恶意的路由器或交换机 公共 Wi-Fi 网络的运营者 攻击者可以使用诸如 Wireshark、tcpdump 等网络抓包工具捕获数据包,直接查看其中的内容。这意味着用户名、密码、信用卡号、私密消息等敏感信息都会暴露在攻击者面前。 篡改风险 明文传输不仅允许攻击者读取内容,还允许他们修改传输的数据。攻击者可以在数据包经过的任何位置插入、删除或修改内容,而接收方难以察觉。例如: 将银行转账金额从 100 元改为 10000 元 修改电子邮件的内容 在网页中插入恶意脚本 替换下载的软件包 冒充风险 由于缺乏身份验证机制,攻击者可以冒充合法的服务器与客户端通信。客户端无法确认与之通信的服务器是否真实可信。这使得钓鱼攻击成为可能:攻击者搭建一个与真实...
变更日志(Changelog)规范
什么是变更日志 变更日志(Changelog)是一个按时间顺序记录项目所有重要变更的文件。它帮助用户、开发者和利益相关者了解每个版本中发生了什么变化,包括新功能、Bug 修复、破坏性变更等。 为什么需要变更日志 用户友好:让用户快速了解新功能、修复的问题和需要注意的变更 版本追溯:帮助定位问题首次出现或修复的版本 团队协作:统一团队对变更的理解和沟通 发布管理:辅助版本发布流程和发布说明的撰写 与 Git Log 的区别 特性 变更日志 Git Log 目标受众 用户、开发者、利益相关者 开发者 内容粒度 功能级别的高级描述 每次提交的详细记录 可读性 高度结构化、易于阅读 技术性强、包含实现细节 维护方式 手动维护或自动化生成 自动记录所有提交 版本关联 按版本组织 按时间顺序 Git Log 记录所有的代码提交,包括内部重构、测试调整等;而变更日志只记录对用户有意义的变更。 Keep a Changelog 规范 Keep a Changelog 是目前最广泛采用的变更日志规范,由 Olivier Lacan 创建。 变更类型分类 Ke...
Kubernetes 核心概念
从 Docker 到 Kubernetes 的演进 Docker 的出现彻底改变了应用程序的打包和部署方式。通过容器化技术,开发人员能够将应用程序及其依赖项打包到一个轻量级的、可移植的容器中,确保了"一次构建,到处运行"的一致性体验。然而,随着容器化应用的规模扩大,单机容器管理的局限性逐渐显现。 在单机环境中,Docker 提供了容器生命周期管理、资源隔离、网络配置等基础功能。但当应用规模扩展到多台服务器时,运维团队面临诸多挑战:跨主机的容器调度、服务发现、负载均衡、故障自愈、滚动升级、资源配额等问题变得日益复杂。手工管理几十甚至上百个容器不仅效率低下,而且容易出错。 容器编排平台应运而生。Kubernetes(K8s)作为容器编排领域的领导者,提供了一个完整的平台,用于自动化部署、扩展和管理容器化应用。它解决了多机环境下的核心问题:自动化调度、服务发现、负载均衡、存储编排、自动扩缩容、滚动更新和回滚、自我修复等。Kubernetes 不仅是一个编排工具,更是一个云原生应用的基础设施平台。 Kubernetes 架构 Kubernetes 采用主从架构,由控制...
跨语言超时机制全解析
从"等不起"到"不想等":跨语言超时机制全解析 “A distributed system is one in which the failure of a computer you didn’t even know existed can render your own computer unusable.” —— Leslie Lamport 在分布式系统中,超时是应用与混沌之间最后一道防线。没有超时的 RPC 调用,如同没有刹车的汽车——迟早会撞上墙。 许多 Java 开发者对超时的认知停留在 Future.get(timeout, unit) 这一层,其底层依赖 LockSupport.parkNanos 和自旋等待。然而,翻阅 HSF/Dubbo 的源码会发现,这些 RPC 框架选择的是 HashedWheelTimer(时间轮)。 这就引出了一个值得深究的问题:为什么不直接用 Future.get 的超时版本?时间轮到底解决了什么问题? 事实上,仅 Java 一门语言就存在三种截然不同的超时实现范式。再放眼 Go、JavaS...
Java 线程池笔记
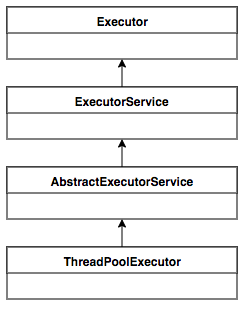
从执行器到线程池(from executor interface to thread pool implementation) Pooling is the grouping together of resources (assets, equipment, personnel, effort, etc.) for the purposes of maximizing advantage or minimizing risk to the users. The term is used in finance, computing and equipment management.——wikipedia “池化”思想不仅仅能应用在计算机领域,在金融、设备、人员管理、工作管理等领域也有相关的应用。 在计算机领域中的表现为:统一管理IT资源,包括服务器、存储、和网络资源等等。通过共享资源,使用户在低投入中获益。除去线程池,还有其他比较典型的几种使用策略包括: 内存池(Memory Pooling):预先申请内存,提升申请内存速度,减少内存碎片。 连接池(Connection Pool...
线程安全与锁优化
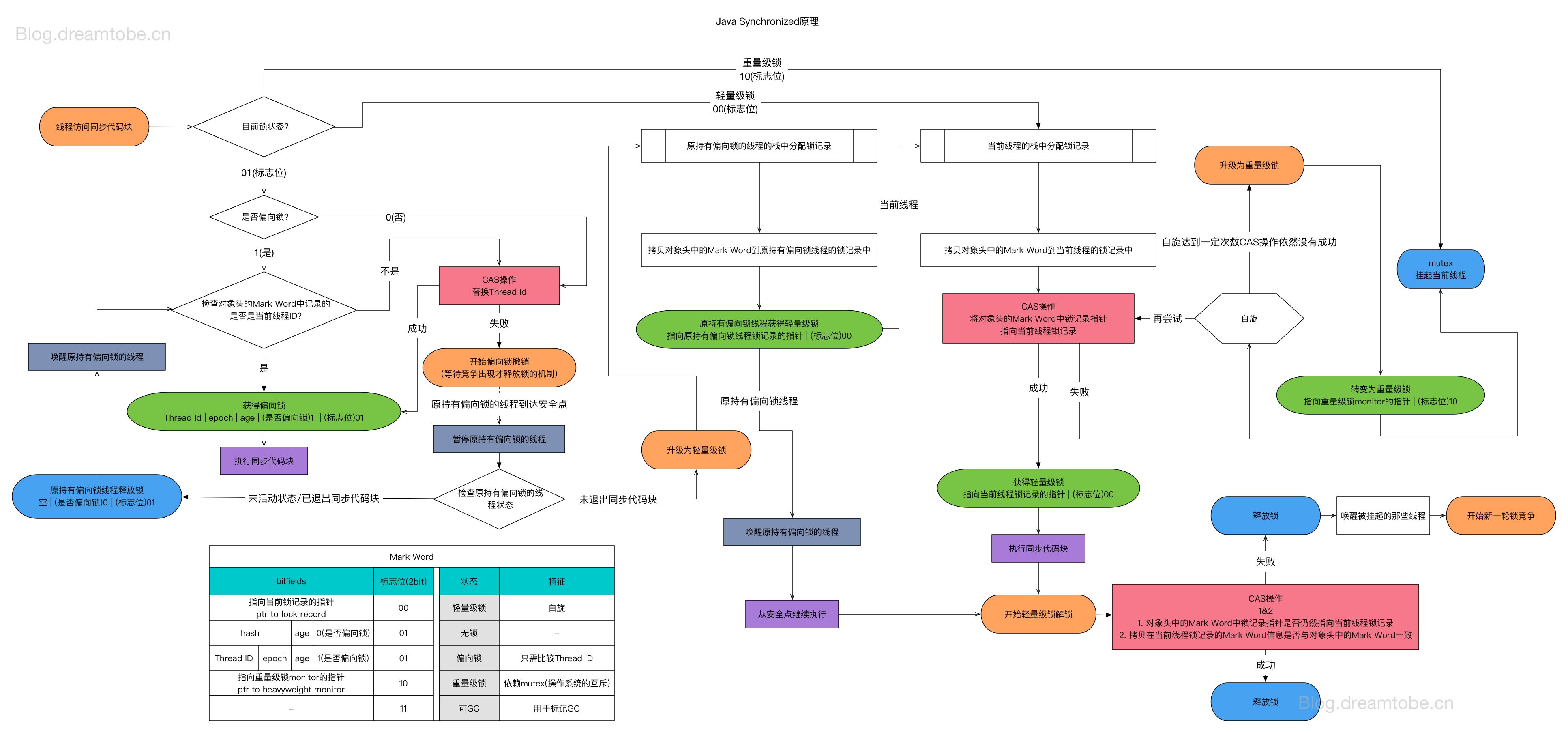
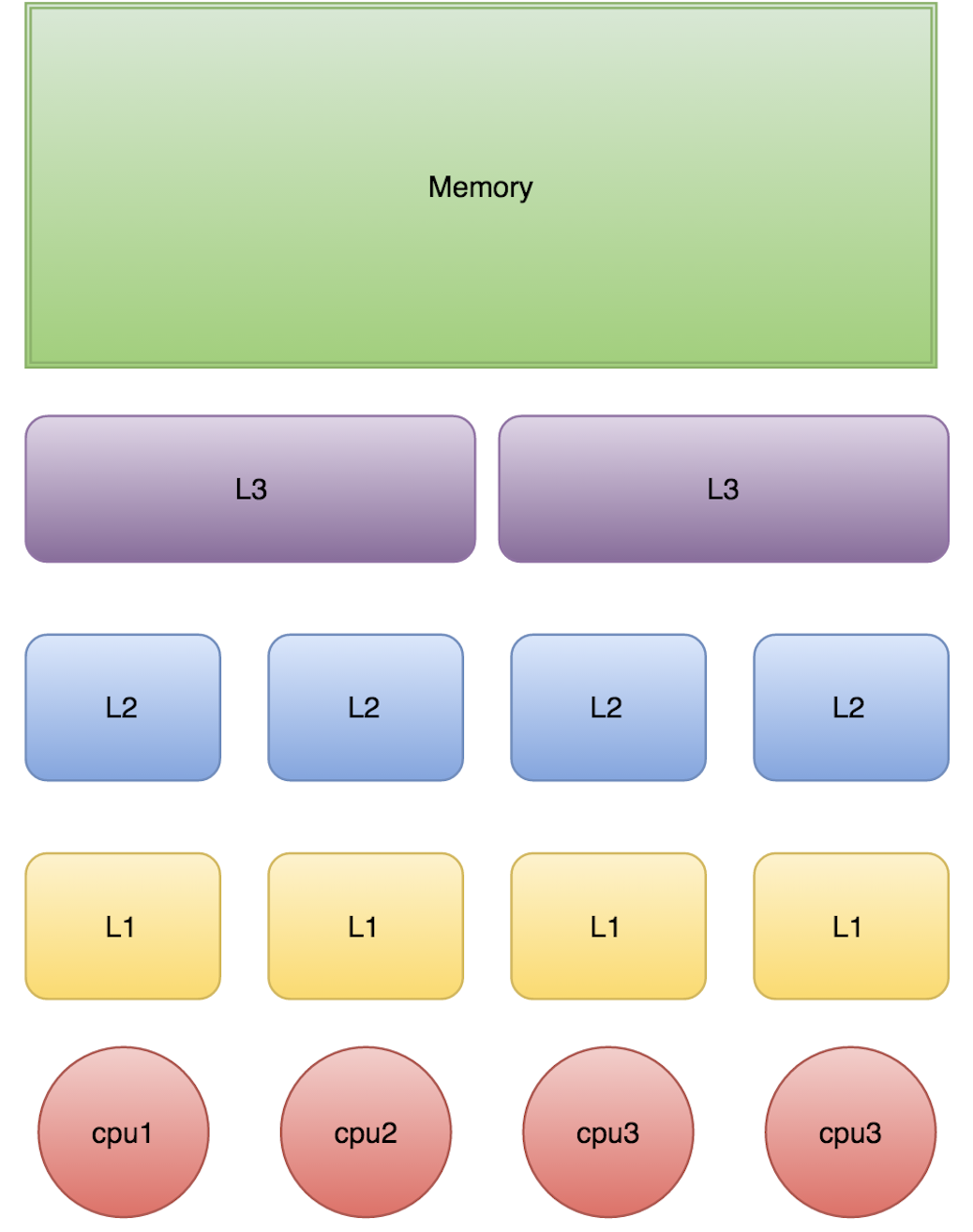
版本说明:本文主要基于 JDK 6 ~ JDK 14 的 HotSpot 虚拟机实现。需要注意的是,从 JDK 15 开始,偏向锁已被默认关闭并标记为废弃(JEP 374)。如果你使用的是 JDK 15+,文中关于偏向锁的内容仅作为历史参考。 线程安全 什么是线程安全 “当多个线程访问一个对象时,如果不用考虑这些线程在运行时环境下的调度和交替执行,也不需要进行额外的同步,或者在调用方法进行任何其他的协调操作,调用这个对象的行为都可以获得正确的结果,那么这个对象就是线程安全的。” 相对的线程安全,可以分成五个等级。但在深入讨论线程安全的分类之前,我们需要先理解 Java 内存模型——它是理解线程安全问题的理论基础。 Java 内存模型基础 Java 内存模型(Java Memory Model,JMM)是 Java 语言规范的一部分,定义了多线程程序中共享变量的访问规则。理解 JMM 是理解线程安全问题的基础。 为什么需要内存模型? 现代计算机系统中,CPU 与主内存之间存在巨大的速度差异。为了弥补这一差距,硬件层面引入了多级缓存(L1、L2、L3 Cache)。这带来了一个问...
无锁队列
Java 一读一写(SPSC):Memory Barrier + Volatile 123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657/** * Single-Producer Single-Consumer (SPSC) 无锁环形队列。 * * <p>原理说明: * - 仅允许一个线程调用 {@code offer()},一个线程调用 {@code poll()}。 * - 由于没有写竞争,无需 CAS;只需保证写操作对消费者可见。 * - 使用两个 volatile 索引(head/tail)建立 happens-before 关系: * 生产者写入元素 → volatile 写 tail → 消费者 volatile 读 tail → 读取元素。 * - 这本质上利用了 Java 内存模型中的“volatile 写-读”内存屏障(StoreLoad), * ...
Java 并发编程笔记
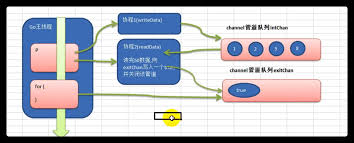
juc.xmind 写在前面的话 并发编程最早的实践都在操作系统里。高层语言的并发模型都要基于底层系统对硬件抽象和并发的设计来设计和实现,不能超出操作系统允许的范围。所谓的高级抽象总体上是简化对 OS 底层机制的复杂调用。 并发与异步 本文聚焦并发(Concurrency),即多任务在同一时间段内的交替或并行执行,核心问题是资源共享、线程同步与协作。 **异步(Asynchronous)**是另一维度:调用方发起操作后不等结果返回即继续执行,通过回调、Future或事件机制获取结果。异步可通过单线程事件循环实现,也可依托多线程并发实现。 二者关系:并发关注"多任务如何执行与协调",异步关注"调用是否阻塞等待"。并发编程常涉及异步,但本文不展开异步编程模式(如响应式流、协程),相关内容请参阅《Java 线程池笔记》。 管程 理论和实践之间是有鸿沟的,要弥合这种鸿沟,通常需要我们去学习别人的实践。比如并发的标准设计思想来自于操作系统里的管程(monitor),我们应当学习管程,进而了解标准的并发模型-管理共享变量和线程(并发任务)间通信的基本...